本文概述了用于图形分析的 Databricks 功能，并介绍了基本图形概念。 图形通常也称为网络，尤其是在研究的特定领域（如社交网络或通信网络）的背景下。
图形是由边缘连接的一组顶点。 顶点通常也称为节点，边缘有时称为链接、关系或弧线。 例如，社交网络表示人员之间的连接。 其他示例包括交通网络，例如城市之间的航班、火车或公共汽车连接，以及电信网络，例如在服务器之间传输互联网流量的电缆。 图形处理也通常用于欺诈或威胁检测和产品建议等领域。 许多业务问题受益于通过图形处理对网络的理解和分析，当与其他分析技术（包括机器学习）结合使用时，它的功能特别强大。
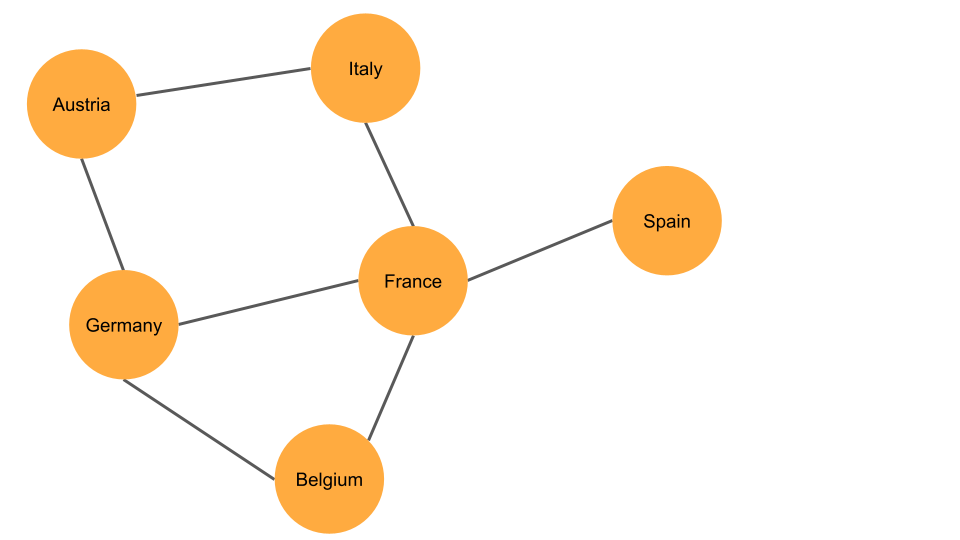
该图显示了一个简单的示例。 此网络中的节点是西欧和中欧的 6 个国家/地区。 图中的线条或边缘表示两个国家/地区共享国界。
Databricks Runtime ML 包含用于解决任何规模问题的网络分析软件包。 对于可在单个计算节点上处理的相对较小的网络，请使用 NetworkX。 对于需要分布式处理的大型网络，请使用 GraphFrames。 还可以根据需要安装其他开放源代码包，或连接到外部合作伙伴和工具进行图形处理和可视化。
本文的其余部分介绍了基本的网络分析概念，并包括使用包 NetworkX 来说明其中一些概念的笔记本。
本部分介绍网络分析的一些基本概念。
在网络分析中，网络或图形由一组节点和一组连接节点的边缘或链接组成。 节点表示正在连接的对象，例如人员或城市。 边缘表示它们之间的连接或关系，例如一起工作的人或有直接连接的火车站。
节点也称为顶点、点或实体。 边缘也称为线条、关系或链接。
网络中的边缘可以表示单向关系，例如在社交网络上关注名人的粉丝，或双向关系（如同事）。 如果边缘可以是单向的，则网络称为有向网络。 如果边缘没有关联的方向，则网络称为无向网络。
边缘可以具有权重。 网络中权重的示例可能是高速公路或电缆的承载能力。
节点的度是与其链接的边缘数。 例如，在上图中，节点“France”有 4 度。
对于有向图，入度是进入节点的边缘数，出度是远离节点的边缘数。
最短路径是两个节点之间的最小距离，需考虑到方向链接并可能需要考虑边缘权重。 例如，在上图中，德国和西班牙节点之间的最短路径是通过法国，路径距离为 2。
集中性是衡量网络中节点重要性的方法。 有几种不同的集中性衡量方法。 节点的度中心性是根据该节点在网络中直接连接的节点的比例来衡量的。 节点的中介中心性是网络中经过该节点的最短路径的一小部分。
网络的度分布是每个度的节点数。 它提供有关网络结构和组织的信息。
网络的直径是任意两个节点之间的最短路径的最大值。 直径等同于网络中节点的最大偏心度。
图形的密度是图形中的边缘数除以可能边缘的总数。 对于无向图，可能的边缘总数为 n(n-1)/2，其中 n 是节点数。 对于有向图，每个边缘都有两个可能的方向，因此可能的边缘总数为 n(n-1)。
大多数真实世界的网络不是随机连接的，而是表现出某种模式和子结构。 网络中的这种涉及人的模式的示例是“小世界现象”，我们观察了紧密关联的子组，以及任何两个节点之间的短平均路径长度。 这些模式在实践中非常常见，并导致大规模图处理中的常见挑战，例如在处理大型图时，需要处理自然产生的数据偏差。
以下示例笔记本使用 NetworkX 包，它内置于用于 ML 的 Databricks Runtime 中，用于演示一些基本的网络分析概念。