Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
Applies to: ✅ Azure Data Explorer ✅ Azure Monitor ✅ Microsoft Sentinel
Applies a polynomial regression from an independent variable (x_series) to a dependent variable (y_series). This function takes a table containing multiple series (dynamic numerical arrays) and generates the best fit high-order polynomial for each series using polynomial regression.
Tip
- For linear regression of an evenly spaced series, as created by make-series operator, use the simpler function series_fit_line(). See Example 2.
- If x_series is supplied, and the regression is done for a high degree, consider normalizing to the [0-1] range. See Example 3.
- If x_series is of datetime type, it must be converted to double and normalized. See Example 3.
- For reference implementation of polynomial regression using inline Python, see series_fit_poly_fl().
Syntax
T | extend series_fit_poly(y_series [, x_series, degree ])
Learn more about syntax conventions.
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| y_series | dynamic |
✔️ | An array of numeric values containing the dependent variable. |
| x_series | dynamic |
An array of numeric values containing the independent variable. Required only for unevenly spaced series. If not specified, it's set to a default value of [1, 2, ..., length(y_series)]. | |
| degree | The required order of the polynomial to fit. For example, 1 for linear regression, 2 for quadratic regression, and so on. Defaults to 1, which indicates linear regression. |
Returns
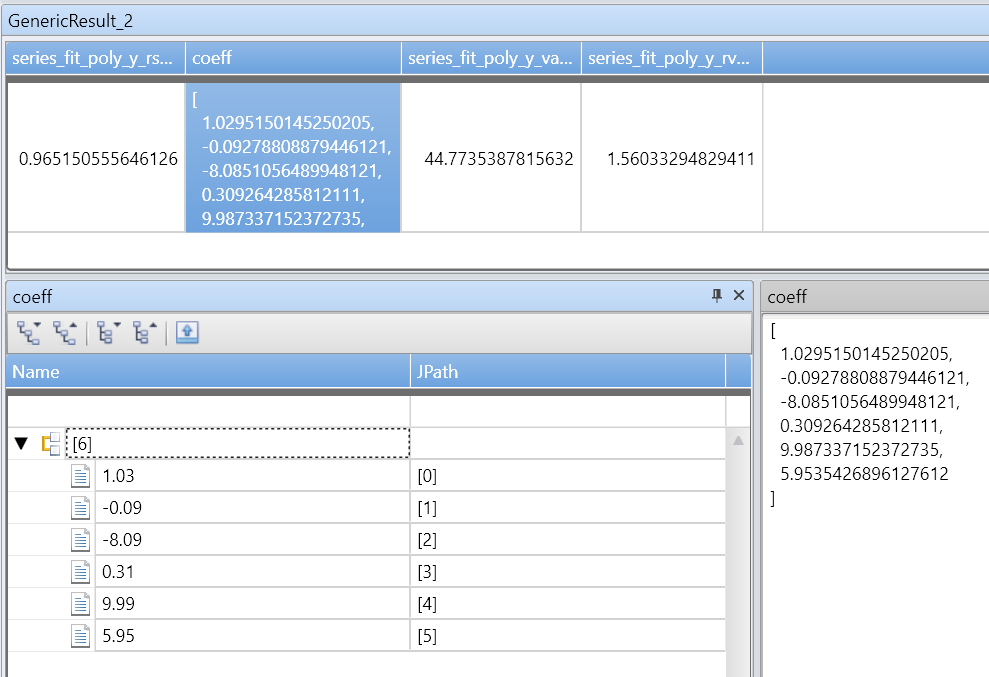
The series_fit_poly() function returns the following columns:
rsquare: r-square is a standard measure of the fit quality. The value's a number in the range [0-1], where 1 - is the best possible fit, and 0 means the data is unordered and doesn't fit any line.coefficients: Numerical array holding the coefficients of the best fitted polynomial with the given degree, ordered from the highest power coefficient to the lowest.variance: Variance of the dependent variable (y_series).rvariance: Residual variance that is the variance between the input data values the approximated ones.poly_fit: Numerical array holding a series of values of the best fitted polynomial. The series length is equal to the length of the dependent variable (y_series). The value's used for charting.
Examples
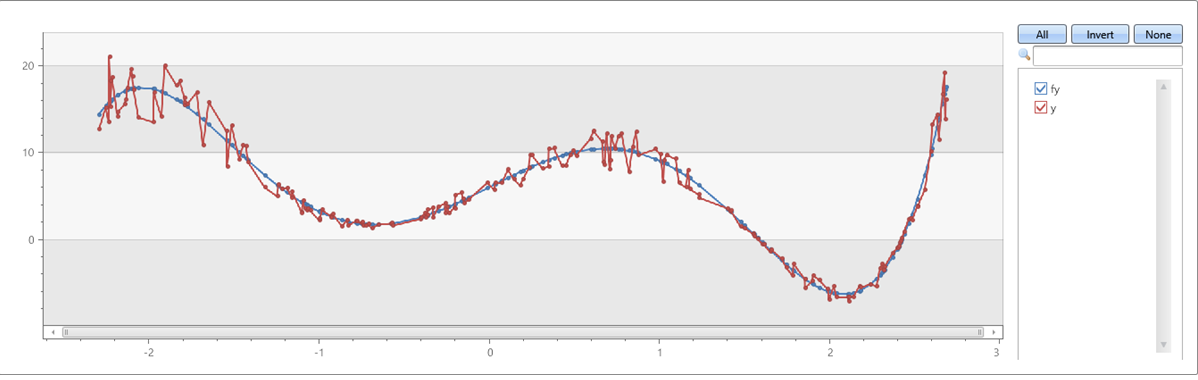
Example 1
A fifth order polynomial with noise on x & y axes:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
Example 2
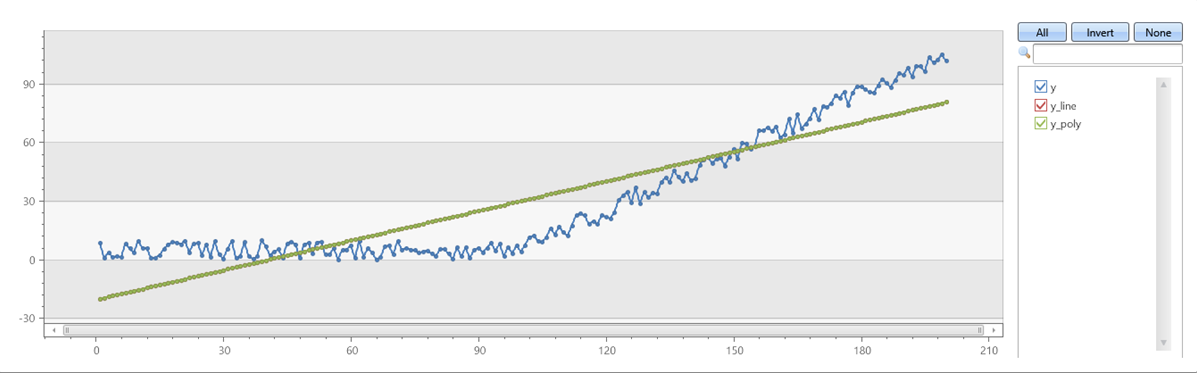
Verify that series_fit_poly with degree=1 matches series_fit_line:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)

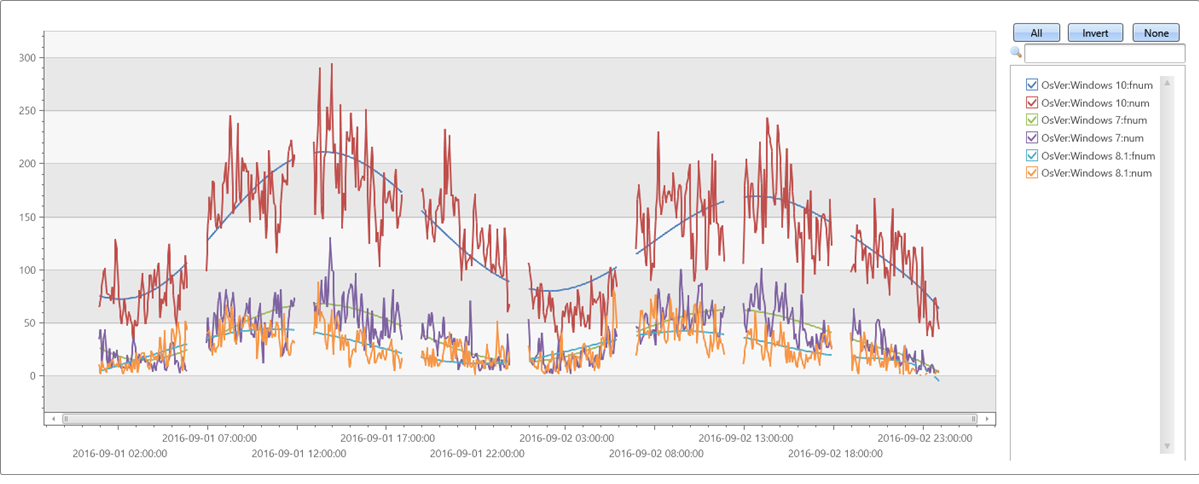
Example 3
Irregular (unevenly spaced) time series:
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)