Nota:
El acceso a esta página requiere autorización. Puede intentar iniciar sesión o cambiar directorios.
El acceso a esta página requiere autorización. Puede intentar cambiar los directorios.
适用范围: Azure CLI ml 扩展 v2(最新版)
Azure CLI ml 扩展 v2(最新版) Python SDK azure-ai-ml v2(最新版)
Python SDK azure-ai-ml v2(最新版)
负责任人工智能(负责任 AI)是一种以安全、可靠和合乎道德的方式开发、评估和部署 AI 系统的方法。 AI 系统是开发和部署它们的人员做出的许多决策的产物。 从系统用途到人们与 AI 系统的交互方式,负责任 AI 有助于主动引导这些决策朝着更有益且更公平的结果发展。 这意味着将人员及他们的目标作为系统设计决策的核心,并尊重公平性、可靠性和透明度等持久价值观。
Microsoft 制定了负责任 AI 标准。 它是根据六项原则生成 AI 系统的框架:公平性、可靠性和安全性、隐私和安全性、包容性、透明度和问责制。 对于 Microsoft 而言,这些原则是负责任且值得信赖的 AI 方法的基石,尤其是随着智能技术在人们日常使用的产品和服务中变得越来越普遍。
本文演示 Azure 机器学习如何支持使开发人员和数据科学家实现和运用上述六项原则的工具。
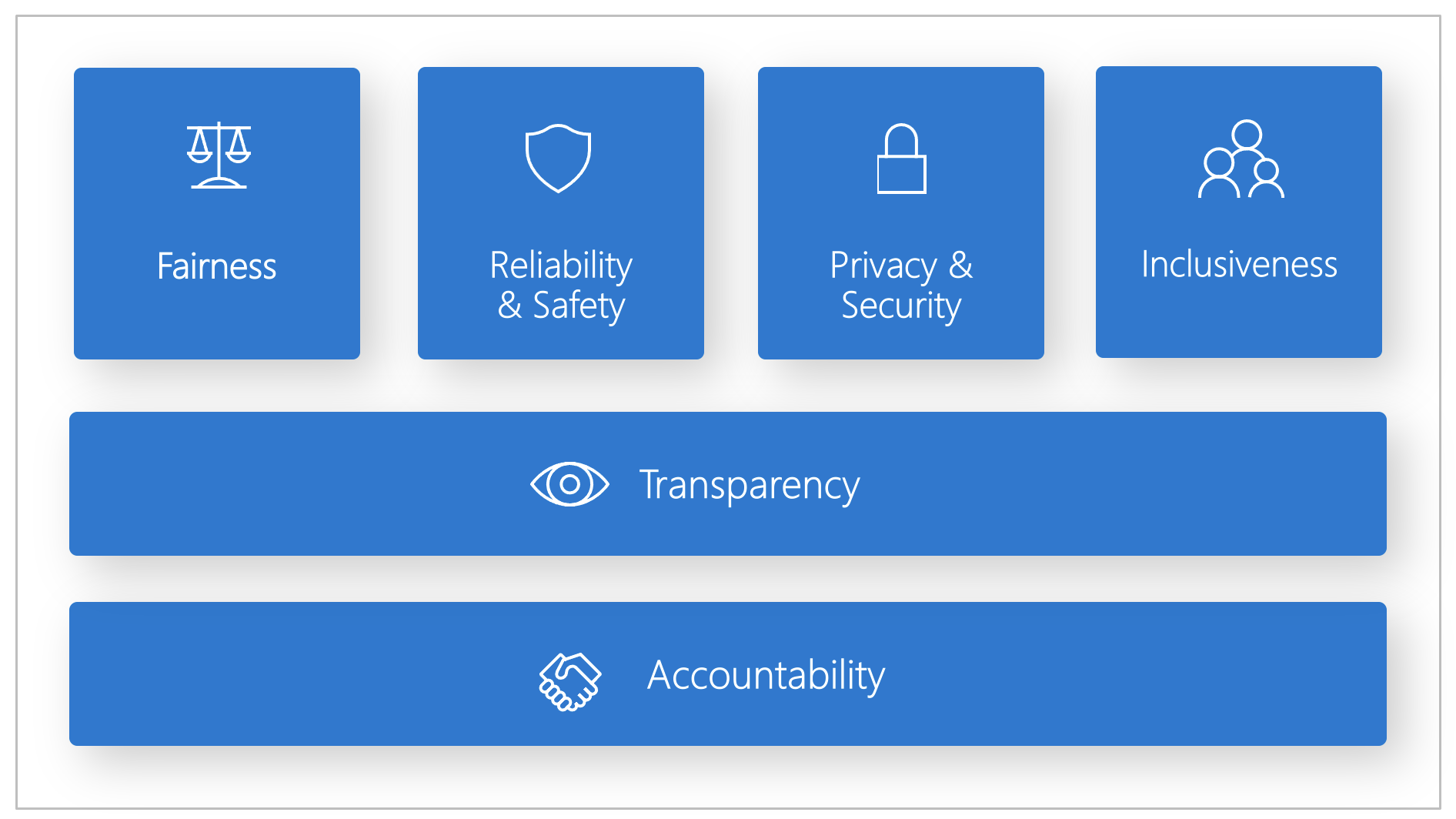
公平性和包容性
AI 系统应该公平对待每个人,并避免以不同的方式影响境况相似的人群。 例如,当 AI 系统为医疗、贷款申请或就业提供指导时,它们应向所有具有相似症状、财务状况或专业资格的人提供相同的建议。
Azure 机器学习中的公平性和包容性:负责任 AI 仪表板的公平性评估组件使数据科学家和开发人员能够在按照性别、种族和年龄等特征定义的敏感群体中评估模型公平性。
可靠性和安全性
为了生成信任,AI 系统可靠、安全且一致地运行是至关重要的。 这些系统应该能够按照最初的设计运行、安全地响应意外情况,并抵御有害操作。 系统的行为方式及它们可处理的各种状况反映了开发人员在设计和测试期间所预计的情况和情形的范围。
Azure 机器学习中的可靠性和安全性:负责任 AI 仪表板的错误分析组件使数据科学家和开发人员能够:
- 深入了解模型的失败分布形式。
- 识别错误率高于整体基准的数据队列(子集)。
当系统或模型对训练数据中的特定人口群体或不经常观察到的输入条件表现不佳时,可能会出现这些差异。
透明度
当 AI 系统有助于制定对人们的生活产生巨大影响的决策时,人们必须了解这些决策是如何做出的。 例如,银行可能会使用 AI 系统来确定某人的资信是否可靠。 公司可能会使用 AI 系统来确定最符合雇佣资格的候选人。
透明度的关键部分在于可解释性:即对 AI 系统及其组件行为的有用解释。 提高可解释性要求利益干系人理解 AI 系统的运行方式及原因。 随后,利益干系人可以确定潜在的性能问题、公平性问题、排他性做法或意外结果。
Azure 机器学习中的透明度:负责任 AI 仪表板的模型可解释性和反事实 what-if 组件使数据科学家和开发人员能够生成人类可理解的模型预测描述。
模型可解释性组件提供了模型行为的多个视图:
- 全局解释。 例如,哪些功能会影响贷款分配模型的总体行为?
- 局部解释。 例如,为何批准或拒绝了客户的贷款申请?
- 选定数据点队列的模型解释。 例如,哪些特征会影响适用于低收入申请人的贷款分配模型的总体行为?
反事实 what-if 组件可以根据机器学习模型对特征更改和扰动的反应方式来理解和调试模型。
Azure 机器学习还支持负责任 AI 记分卡。 记分卡是一种可自定义的 PDF 报告,开发人员可以轻松配置、生成和下载它,并将它与技术和非技术利益干系人共享,从而为他们提供有关数据集和模型运行状况的信息、实现合规性并建立信任。 此记分卡还可用于审核评论,从而揭示机器学习模型的特征。
隐私和安全
随着 AI 变得越来越普遍,保护隐私以及保护个人和商业信息变得越来越重要和复杂。 对于 AI,需要密切关注隐私和数据安全,因为访问数据对于 AI 系统做出有关人类的准确、明智的预测和决策而言至关重要。 AI 系统必须遵守以下隐私法:
- 要求数据的收集、使用和存储具有透明度。
- 要求使用者进行适当控制来选择其数据的使用方式。
Azure 机器学习中的隐私和安全性:Azure 机器学习使管理员和开发人员能够创建符合公司策略的安全配置。 借助 Azure 机器学习和 Azure 平台,用户可以:
- 限制用户帐户或组对资源和操作的访问。
- 限制传入和传出网络通信。
- 加密传输中的数据和静态数据。
- 扫描漏洞。
- 应用和审核配置策略。
Microsoft 还创建了两个开源包,可以进一步支持实现隐私和安全性原则:
SmartNoise:差别隐私是一组系统和做法,有助于保持个人数据的安全性和私密性。 在机器学习解决方案中,可能需要差别隐私来实现监管合规性。 SmartNoise 是一个开源项目(Microsoft 参与了联合开发),其中包含用于生成全局差别隐私系统的组件。
Counterfit:Counterfit 是一个开源项目,其中包含命令行工具和通用自动化层,使开发人员能够模拟针对 AI 系统的网络攻击。 任何人都可以下载该工具并通过 Azure CLI 进行部署以在浏览器中运行,或者在 Anaconda Python 环境中进行本地部署。 它可以评估托管在各种云环境、本地或边缘位置的 AI 模型。 该工具不区分 AI 模型,且支持各种数据类型,包括文本、图像或通用输入。
问责
设计和部署 AI 系统的人必须对其系统的运行负责。 组织应利用行业标准制定问责规范。 这些规范可以确保 AI 系统不会成为影响人们生活的任何决策的最终权威。 它们还可以确保人类对其他高度自治的 AI 系统保持有意义的控制。
Azure 机器学习中的问责制:机器学习操作 (MLOps) 基于可提高 AI 工作流效率的 DevOps 原则和做法。 Azure 机器学习提供以下 MLOps 功能,以便更好地实现 AI 系统的问责:
- 从任意位置注册、打包和部署模型。 还可以跟踪使用模型所需的关联元数据。
- 捕获端到端机器学习生命周期的监管数据。 记录的世系信息可以包括模型的发布者、做出更改的原因,以及在生产环境中部署或使用模型的时间。
- 针对机器学习生命周期中的事件发出通知和警报。 示例包括试验完成、模型注册、模型部署和数据偏移检测。
- 监控应用程序的操作问题和与机器学习相关的问题。 比较训练与推理之间的模型输入,浏览特定于模型的指标,以及针对机器学习基础结构提供监视和警报。
除了 MLOps 功能外,Azure 机器学习中的负责任 AI 记分卡通过启用跨利益干系人的通信来创建问责制。 记分卡还可以创建问责制,方法是授权开发人员配置、下载并与其技术和非技术利益干系人共享模型运行状况见解,这些见解与 AI 数据和模型运行状况相关。 共享这些见解有助于建立信任。
机器学习平台还通过以下方式为业务决策提供信息来帮助做出决策:
- 数据驱动的见解,只需使用历史数据即可帮助利益干系人了解因果处理对结果的影响。 例如,“药物如何影响患者的血压?”这些见解通过负责任 AI 仪表板的因果推理组件提供的。
- 模型驱动的见解,可以回答用户的问题(例如“下次我能做些什么才能从你的 AI 得到不同结果?”),使用户能够采取措施。 此类见解通过负责任 AI 仪表板的反事实 what-if 组件提供给数据科学家。
后续步骤
- 有关如何在 Azure 机器学习中实施负责任 AI 的详细信息,请参阅负责任 AI 仪表板。
- 了解如何通过 CLI 和 SDK 或 Azure 机器学习工作室 UI 生成负责任 AI 仪表板。
- 了解如何根据在负责任 AI 仪表板中观察到的见解生成负责任 AI 记分卡。
- 了解用于根据六项关键原则生成 AI 系统的负责任 AI 标准。